Monday, December 12, 2005
Best tattoo ever
The Mandelbrot Set!
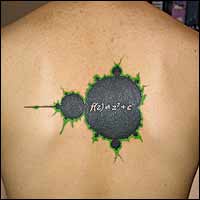
(via "Revenge of the Tattooed Nerds")
I was obsessed with the Mandelbrot set when I was a kid. A friend of mine (Wes) showed me a Mandelbrot set program on his Commodore 64 as well as the computer magazine article that posted the algorithm for it. Determined, I ported it to BASIC on my Apple //c. I succeeded but the machine at the time didn't have the chops for speed, so some of the sets took all night (or multiple days) to render. If that wasn't geeky enough, later on in my high school career I made a similar Mandelbrot plotter on my TI-85. Nowadays, an everyday web browser can render the Mandelbrot set more quickly than I ever could, even in JavaScript.
What's the big deal? Well for me the fascination was that something so complex as the Mandebrot set could be represented by such a simple-seeming equation: z = z2 + c. I think the beautiful imagery that arises from such a simple equation explains its enduring appeal. It is one of the things that really inspired me to get into more math as a kid (such inspiration was of course much evaporated by the time I got to college).
A very interesting modern variation is called the "Buddhabrot":


The Buddhabrot is featured on complexification.net, a fascinating "gallery of computation" focusing on very cool mathematical eye candy, including some algorithms that are featured in the wonderful xscreensaver program. Xscreensaver is the evil eye candy screensaver that runs on my Linux machines - the program is a fantastic gallery of fun algorithmic displays put together by Jamie Zawinski, one of the original Netscape luminaries (he helped write v1.0 of the Netscape browser for Unix - nowadays he seems to have given up on software altogether by running a nightclub in San Francisco).
Speaking of Mandelbrot variations, this one's pretty. Ooh, shiny. (via this fractal gallery). Puts my monochrome (green and black) Apple //c fractal display to great shame.

(via "Revenge of the Tattooed Nerds")
I was obsessed with the Mandelbrot set when I was a kid. A friend of mine (Wes) showed me a Mandelbrot set program on his Commodore 64 as well as the computer magazine article that posted the algorithm for it. Determined, I ported it to BASIC on my Apple //c. I succeeded but the machine at the time didn't have the chops for speed, so some of the sets took all night (or multiple days) to render. If that wasn't geeky enough, later on in my high school career I made a similar Mandelbrot plotter on my TI-85. Nowadays, an everyday web browser can render the Mandelbrot set more quickly than I ever could, even in JavaScript.
What's the big deal? Well for me the fascination was that something so complex as the Mandebrot set could be represented by such a simple-seeming equation: z = z2 + c. I think the beautiful imagery that arises from such a simple equation explains its enduring appeal. It is one of the things that really inspired me to get into more math as a kid (such inspiration was of course much evaporated by the time I got to college).
A very interesting modern variation is called the "Buddhabrot":


The Buddhabrot is featured on complexification.net, a fascinating "gallery of computation" focusing on very cool mathematical eye candy, including some algorithms that are featured in the wonderful xscreensaver program. Xscreensaver is the evil eye candy screensaver that runs on my Linux machines - the program is a fantastic gallery of fun algorithmic displays put together by Jamie Zawinski, one of the original Netscape luminaries (he helped write v1.0 of the Netscape browser for Unix - nowadays he seems to have given up on software altogether by running a nightclub in San Francisco).
Speaking of Mandelbrot variations, this one's pretty. Ooh, shiny. (via this fractal gallery). Puts my monochrome (green and black) Apple //c fractal display to great shame.
